
Strap on your thinking caps, because there are 20 blanks to fill in, and only one way to do it right.
Growing up as a youngest child, I often found it sort of frustrating that everyone else in the family knew more about the world than I did. That said, I don’t think I’d have felt any smarter if I’d had a younger brother like Japanese Twitter user Aty’s.
Aty (@aty_carbuncle) recently shared a math puzzle created by his younger brother, who’s in the first year of junior high school, meaning he’s 12 or 13. Little Bro wanted Big Bro to fill in the blanks on a simple long division problem…or at least it would have been simple if it didn’t have 20 blanks to fill in!
中一の弟作。
— 立方体 (@aty_carbuncle) February 3, 2020
穴だらけながら答えが1つに定まる良問です。やるやん pic.twitter.com/s0jChgVuK1
Yep, aside from the 6 and the 0 in the computation section, and the decimal point in the quotient, everything else is up to you. With so many blanks, you might think there’re dozens of possible answers, but it turns out there’s only one possible solution.
I’ll give you a few seconds to try to figure it out/curse loudly in frustration at your screen.
…
All good? Okay. Like I said, there’s only one way to answer this question, and Aty, who was up to the challenge, explains it here.
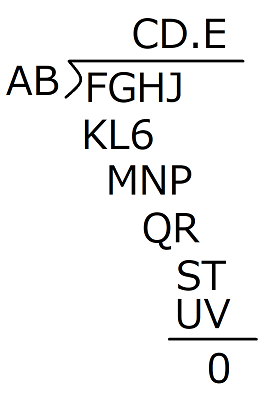
Of course, this is a math problem, not a linguistic one, so let’s walk through Aty’s steps in English. Before we get started, though, let’s rewrite the problem using Latin letters for each unknown digit instead of the Japanese katakana text from Aty’s handwritten notes.
Because of the problem’s complexity, for notation purposes we’re going to treat each variable simply as its digit. For example, AB is a two-digit number, not the product of A times B. Also, it’s possible that some of the unknowns will end up being the same number (A and B could both be 1, for example).
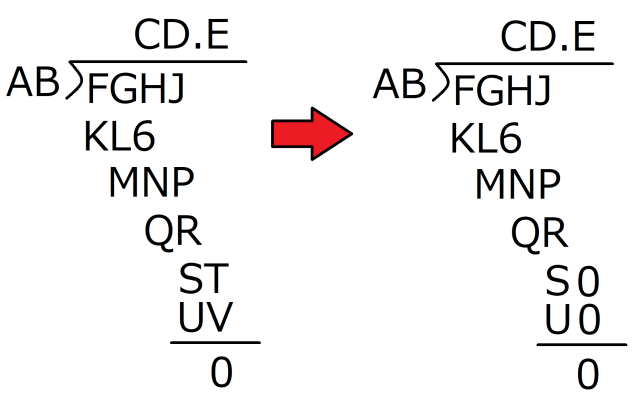
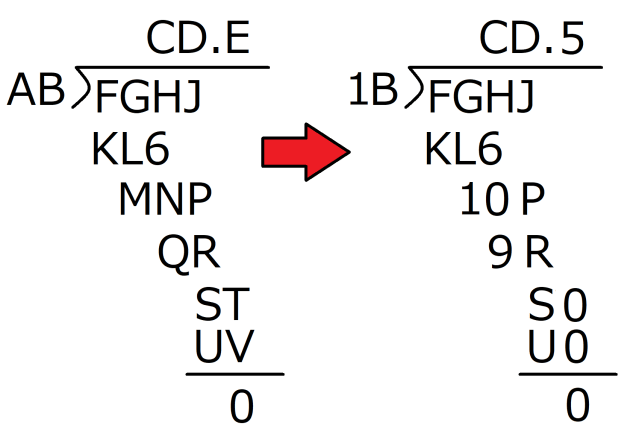
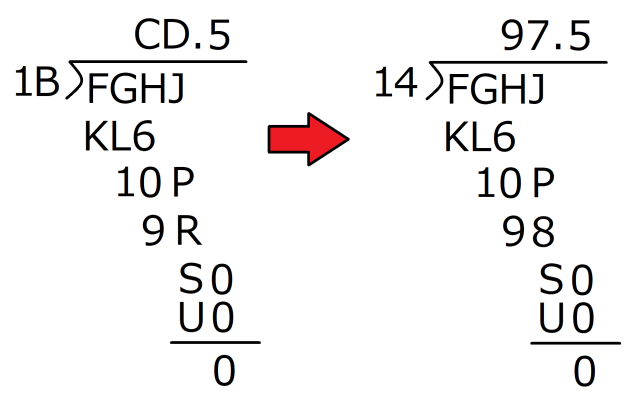
Step 1: You actually need to start at the end, since the given zero is the key to the whole thing. Since T is being added as the quotient moves past the decimal point, T has to be zero, and in order to be the end of the calculation, so does V. Knowing that, let’s update the puzzle.
Step 2: Going back to the original setup, AB x E = UV, and since we figured out that V = 0, we can also say that AB x E = U0, and that in turn means that the ones digit of B x E has to 0. If B x E gives us a 0 for the ones digit, the possibilities for B and E are (2, 5), (4, 5), (6, 5), (8, 5), (5,2), (5, 4), (5, 6), and (5, 8).
B can’t be 5, though. Because of the 6 we’re given at the start of the problem, we know that AB x C = KL6. If B were 5, then AB times anything could only end in a 5 or 0. Since B can’t be 5, we can cross off half the combinations, and now the possibilities for B and E are (2, 5), (4, 5), (6, 5) and (8, 5).
But wait, we know that AB x E = U0, right? If B isn’t 5, then the only way AB x E = U0 is possible is for E to be 0 or 5. But E can’t be 0, because it’s being added after the decimal point to complete the division. You wouldn’t need to do that if E were 0, so E has to be 5 (as for B, we’re going to come back to it later).
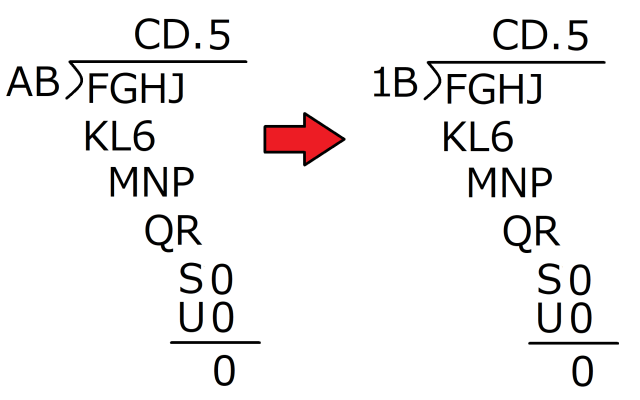
Step 3: Now let’s figure out A. What would happen if A were 2 or larger? Since E is 5, A being 2 or more would mean that AB x E, or AB x 5, would end up as at least 100, if not more. In any case, it’d be a three-digit number. But we know that AB x 5 = U0, a two-digit number. So A can’t be 2 or larger, and it also can’t be 0, since it’s the largest digit in the divisor (i.e. there’d be no point to writing AB to start the question if A was 0). So by process of elimination, A has to be 1.
Step 4: Next up, we know MNP – QR = S (remember, the 0 next to S, which started out as the unknown T, was only added as a drop-down when the calculation got past the decimal point). So we’ve got a three-digit number (MNP), and when we subtract a two-digit number (QR), the difference is a one-digit number (S). This eliminates a lot of possibilities.
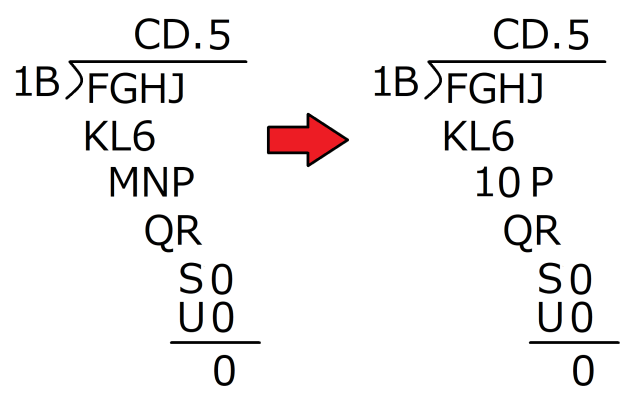
QR is a two-digit number, so it can’t be any bigger than 99, which means MNP can’t be any bigger than 108. If it were, subtracting 99 wouldn’t give us a one-digit number. At the same time, MNP obviously can’t be any smaller than 100. So while P is still a mystery (it has to be something between 0 and 8, though) right now, we can be absolutely certain that M is 1 and N is 0.
Step 5: Likewise, we can figure out that QR has to be at least 91, because if it were any smaller, subtracting it from a three-digit number wouldn’t give us a one-digit number. Once again, R is a momentary mystery, but at least we know that Q is 9, and we know that no matter what R eventually ends up being, it can’t be 0 (since we need to subtract at least 91 from the smallest possible three-digit number, 100, to get a one-digit one).
We’re now about half-way through the solution, so let’s take a short break for a nice cup of tea.
Okay, let’s finish this thing off! Remember, here’s what we’ve figured out so far.
We also know that P is some number between 0 and 8 (i.e. it can’t be 9), and R is some number between 1 and 9 (it can’t be 0).
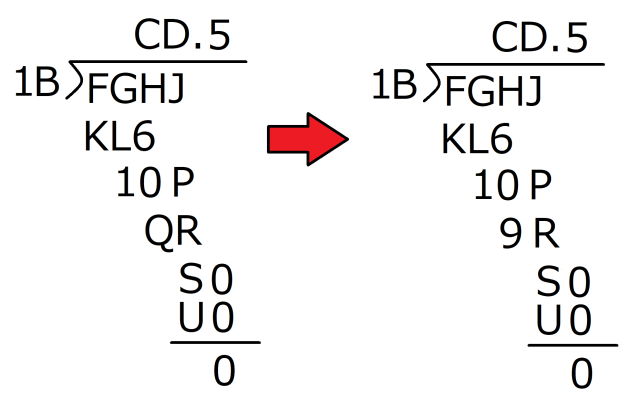
Step 6: Hey, remember all the way back in Step 2, where we found that the possibilities for B and E were (2, 5), (4, 5), (6, 5), (8, 5), (5,2), (5, 4), (5, 6), and (5, 8)? We eventually figured out that E has to be 5, so the remaining possible B and E combinations are (2, 5), (4, 5), (6, 5) and (8, 5). In other words, B has to be 2, 4, 6, or 8, so which one is it?
We know 1B x C = KL6, 1B x D = 9R, and that 9 has to be greater than 0. So let’s plug in the possibilities for B and see what happens.
● If B is 2, then we’d have 12 x C = KL6. But the only way 12 times a single-digit number would give us a three-digit number would be 12 x 9, which is 108. That doesn’t fit with KL6, so 2 is out as a possibility for B.
● If B is 6, we’d have 16 x C = KL6. Once again, there’s no value for C that works (the 16 x C three-digit possible values are 112, 128, and 144; once again, none have a 6 in the ones digit). So we can cross off 6.
● If B is 8, initially things look pretty good. 18 x C = KL6 works if C is 7 (the product becomes 126). But what about 18 x D = 9R? There’s only one way to multiply 18 by a single number and get a product with a 9 for the tens digit, and that’s to multiply it by 5, which gives you 90. But remember, back in Step 5 we figured out that R can’t be 0, so we have to eliminate 8 too.
▼ Anybody need another cup of tea?
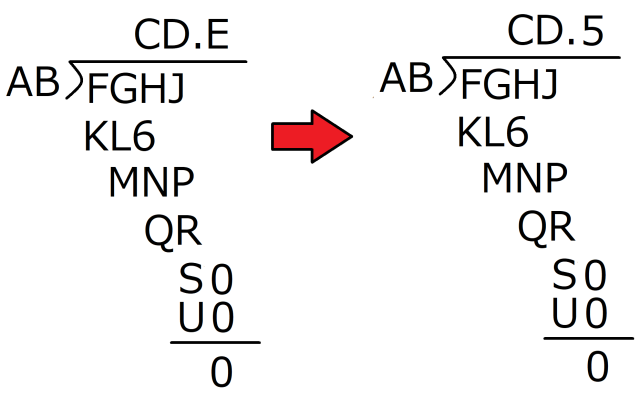
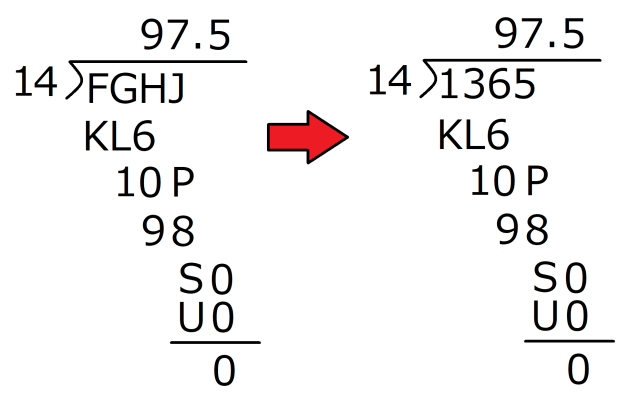
That makes 4 our last remaining hope for B. Fingers crossed, let’s see if it meets all the requirements (1B x C = KL6, 1B x D = 9R, R has to be greater than 0).
Sure enough, 14 x C = KL6 works if C = 9 (the product is 126), and 14 x D = 9R works if D = 7, which gives us the product of 98, in which case R is 8, clearing the “R can’t be 0” hurdle! What’s more, those are the only possible combinations for B, C, D, and R, so now we can plug all four of those numbers into the puzzle together.
At this point, we’ve still got nine blanks to fill in, but now that we’ve got the complete quotient and divisor, the rest is a snap. 14 x 97.5 has to equal FGHJ, so those digits can only be 1365.
If you’ve come this far, I’m guessing you don’t need any refreshers on how to do the basic division that’s left, so let’s turn things back over to Aty for his handwritten final answer.
解答解説です(再)
— 立方体 (@aty_carbuncle) February 5, 2020
条件をたくさん見つけてどれだけシンプルな場合分けに持ち込めるかがカギですね pic.twitter.com/Kz7pfYIF2B
Basically, solving the puzzle requires you to be a mathematical Sherlock Holmes, eliminating the numerical impossibilities one by one until you’re left with the one and only truth. “This was a well-designed question. Nicely done,” Aty later tweeted, showing he’s as skilled at understatement as he is puzzle-solving. And as mentally satisfying as it was to tag along on the path to the solution, it’s also scary to think of what sort of brain teasers the younger math whiz will come up with next.
Source: Twitter/@aty_carbuncle via Jin
Top image: Pakutaso/SoraNews24
Insert images: Twitter/@aty_carbuncle, SoraNews24, Wikipedia/Arria Belli, Pakutaso
● Want to hear about SoraNews24’s latest articles as soon as they’re published? Follow us on Facebook and Twitter!
Following Casey on Twitter is likely to make you feel smarter by comparison.

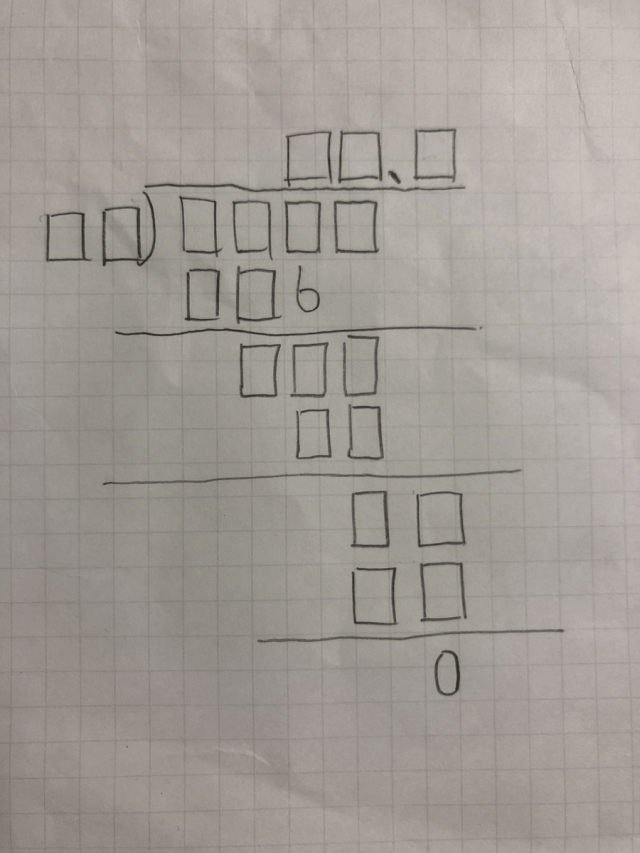



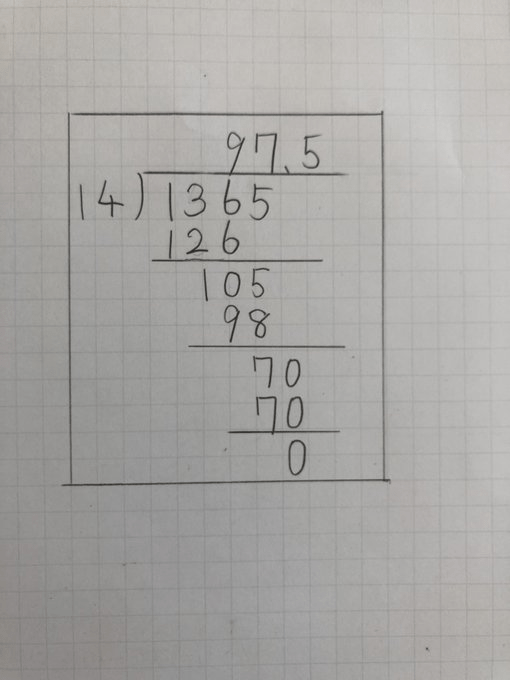
 Customizable minimalistic plastic bonsai trees let you enjoy zen gardening without all the fuss
Customizable minimalistic plastic bonsai trees let you enjoy zen gardening without all the fuss Boys’ love manga categorized into more than 30 sub-genres at mainstream Tokyo bookstore
Boys’ love manga categorized into more than 30 sub-genres at mainstream Tokyo bookstore Japanese breast size study shows rapid growth in previously smallest-busted region of county
Japanese breast size study shows rapid growth in previously smallest-busted region of county Wow, literature is cute! Hiroshima library designs anime mascots for decimal classifications
Wow, literature is cute! Hiroshima library designs anime mascots for decimal classifications Japanese elementary school student teaches us how to solve a difficult maths problem
Japanese elementary school student teaches us how to solve a difficult maths problem Foreigner’s request for help in Tokyo makes us sad for the state of society
Foreigner’s request for help in Tokyo makes us sad for the state of society Japanese city loses residents’ personal data, which was on paper being transported on a windy day
Japanese city loses residents’ personal data, which was on paper being transported on a windy day Seaside scenery, history, and so many desserts on Yokohama’s Akai Kutsu【Japan Loop Buses】
Seaside scenery, history, and so many desserts on Yokohama’s Akai Kutsu【Japan Loop Buses】 Should you add tartar sauce to Japanese curry rice? CoCo Ichi makes diners an unusual offer
Should you add tartar sauce to Japanese curry rice? CoCo Ichi makes diners an unusual offer Red light district sushi restaurant in Tokyo shows us just how wrong we were about it
Red light district sushi restaurant in Tokyo shows us just how wrong we were about it Akihabara pop-up shop sells goods made by Japanese prison inmates
Akihabara pop-up shop sells goods made by Japanese prison inmates Ghibli Park now selling “Grilled Frogs” from food cart in Valley of Witches
Ghibli Park now selling “Grilled Frogs” from food cart in Valley of Witches Princesses, fruits, and blacksmiths: Study reveals the 30 most unusual family names in Japan
Princesses, fruits, and blacksmiths: Study reveals the 30 most unusual family names in Japan Harajuku Station’s beautiful old wooden building is set to return, with a new complex around it
Harajuku Station’s beautiful old wooden building is set to return, with a new complex around it Japanese company starts project to restore Nakagin Capsules to capsule hotel
Japanese company starts project to restore Nakagin Capsules to capsule hotel McDonald’s new Happy Meals offer up cute and practical Sanrio lifestyle goods
McDonald’s new Happy Meals offer up cute and practical Sanrio lifestyle goods Japanese ramen restaurants under pressure from new yen banknotes
Japanese ramen restaurants under pressure from new yen banknotes French Fries Bread in Tokyo’s Shibuya becomes a hit on social media
French Fries Bread in Tokyo’s Shibuya becomes a hit on social media Studio Ghibli releases new action figures featuring Nausicaä of the Valley of the Wind characters
Studio Ghibli releases new action figures featuring Nausicaä of the Valley of the Wind characters New private rooms on Tokaido Shinkansen change the way we travel from Tokyo to Kyoto
New private rooms on Tokaido Shinkansen change the way we travel from Tokyo to Kyoto Tokyo Tsukiji fish market site to be redeveloped with 50,000-seat stadium, hotel, shopping center
Tokyo Tsukiji fish market site to be redeveloped with 50,000-seat stadium, hotel, shopping center All-you-can-drink Starbucks and amazing views part of Tokyo’s new 170 meter-high sky lounge
All-you-can-drink Starbucks and amazing views part of Tokyo’s new 170 meter-high sky lounge Beautiful Ghibli sealing wax kits let you create accessories and elegant letter decorations【Pics】
Beautiful Ghibli sealing wax kits let you create accessories and elegant letter decorations【Pics】 Studio Ghibli releases Kiki’s Delivery Service chocolate cake pouches in Japan
Studio Ghibli releases Kiki’s Delivery Service chocolate cake pouches in Japan New definition of “Japanese whiskey” goes into effect to prevent fakes from fooling overseas buyers
New definition of “Japanese whiskey” goes into effect to prevent fakes from fooling overseas buyers Our Japanese reporter visits Costco in the U.S., finds super American and very Japanese things
Our Japanese reporter visits Costco in the U.S., finds super American and very Japanese things Studio Ghibli unveils Mother’s Day gift set that captures the love in My Neighbour Totoro
Studio Ghibli unveils Mother’s Day gift set that captures the love in My Neighbour Totoro More foreign tourists than ever before in history visited Japan last month
More foreign tourists than ever before in history visited Japan last month New Pokémon cakes let you eat your way through Pikachu and all the Eevee evolutions
New Pokémon cakes let you eat your way through Pikachu and all the Eevee evolutions Sales of Japan’s most convenient train ticket/shopping payment cards suspended indefinitely
Sales of Japan’s most convenient train ticket/shopping payment cards suspended indefinitely Sold-out Studio Ghibli desktop humidifiers are back so Totoro can help you through the dry season
Sold-out Studio Ghibli desktop humidifiers are back so Totoro can help you through the dry season Japanese government to make first change to romanization spelling rules since the 1950s
Japanese government to make first change to romanization spelling rules since the 1950s Ghibli founders Toshio Suzuki and Hayao Miyazaki contribute to Japanese whisky Totoro label design
Ghibli founders Toshio Suzuki and Hayao Miyazaki contribute to Japanese whisky Totoro label design Doraemon found buried at sea as scene from 1993 anime becomes real life【Photos】
Doraemon found buried at sea as scene from 1993 anime becomes real life【Photos】 Tokyo’s most famous Starbucks is closed
Tokyo’s most famous Starbucks is closed One Piece characters’ nationalities revealed, but fans have mixed opinions
One Piece characters’ nationalities revealed, but fans have mixed opinions We asked a Uniqlo employee what four things we should buy and their suggestions didn’t disappoint
We asked a Uniqlo employee what four things we should buy and their suggestions didn’t disappoint Japanese lingerie saleswoman gives Internet a lesson in what bust sizes look like in real life
Japanese lingerie saleswoman gives Internet a lesson in what bust sizes look like in real life Can our reporters tell fancy specialty store camembert cheese from the convenience store stuff?
Can our reporters tell fancy specialty store camembert cheese from the convenience store stuff? Can our writers’ taste buds pick out the luxury kamaboko fish cake from these two?
Can our writers’ taste buds pick out the luxury kamaboko fish cake from these two? Learn Japanese through ridiculous manga: Death Vote 【Episode #6】
Learn Japanese through ridiculous manga: Death Vote 【Episode #6】 Can our writers tell the difference between cheesecake from a luxury hotel and a factory?
Can our writers tell the difference between cheesecake from a luxury hotel and a factory? Learn Japanese through ridiculous manga: Narutoe 【Episode #2】
Learn Japanese through ridiculous manga: Narutoe 【Episode #2】 Artist blows our minds by swapping clothing between Sailor Moon and Dragon Ball characters
Artist blows our minds by swapping clothing between Sailor Moon and Dragon Ball characters Test your knowledge of Japanese convenience stores with this katakana puzzle
Test your knowledge of Japanese convenience stores with this katakana puzzle Six ways science-minded and art-minded Japanese people see the world differently
Six ways science-minded and art-minded Japanese people see the world differently All-you-can-eat yakiniku in Shinjuku for less than 10 bucks!
All-you-can-eat yakiniku in Shinjuku for less than 10 bucks! Do expensive 10,000 yen Japanese cherries taste better than cheap ones from the supermarket?
Do expensive 10,000 yen Japanese cherries taste better than cheap ones from the supermarket? USJ unveils its Halloween lineup, including some first-ever Pokémon food and fun collaborations
USJ unveils its Halloween lineup, including some first-ever Pokémon food and fun collaborations 7 Halloween-themed afternoon teas you won’t want to miss this year
7 Halloween-themed afternoon teas you won’t want to miss this year Can our foodie reporters tell the difference between two brands of tofu with a huge price gap?
Can our foodie reporters tell the difference between two brands of tofu with a huge price gap? New school in Iraq to provide a Japanese-style education
New school in Iraq to provide a Japanese-style education
Leave a Reply